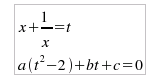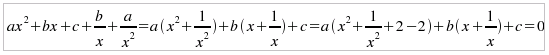Equazioni.

Equazioni intere

Un'equazione algebrica (o polinomiale) ha sempre la forma, o può essere ridotta alla forma:

P(x) = 0

ove P(x) è un polinomio nella variabile x di grado qualsiasi.

Contrariamente alle espressioni algebriche, che nel linguaggio della logica sono trattate come proposizioni, le equazioni rappresentano sempre un generico problema tradotto in termini matematici e le eventuali soluzioni individuano i valori della variabile che risolvono tale problema. In altre termini, le soluzioni di un'equazione sono quei valori della variabile x che trasformano l'equazione P(x) = 0 in un'uguaglianza vera (del tipo P(a) = 0, se a è una soluzione).

Le equazioni si risolvono applicando le due proprietà invariantive delle uguaglianze/equazioni:

I proprietà invariantiva:

Un'uguaglianza (o un'equazione) si trasforma in una equivalente (cioè con le stesse soluzioni) se si sommano (o sottraggono) ad ambo i membri stesse quantità (positive o negative).

La I proprietà si applica ai termini dell'equazione.

La I proprietà comporta il cambio di segno quando un termine viene trasportato da un membro all'altro dell'equazione:

x + a = 0 → x + a – a = -a → x = - a

II proprietà invariantiva:

Un'uguaglianza (o un'equazione) si trasforma in una equivalente (cioè con le stesse soluzioni) se si moltiplicano (o dividono) ambo i membri per una stessa quantità (positiva o negativa) purchè essa sia diversa da zero.

La II proprietà si applica ai fattori dell'equazione.

La complessità dei metodi di risoluzione delle equazioni dipende innanzitutto dal grado massimo a cui è elevata l'incognita. Fin dall'antichità sono noti metodi di risoluzione delle equazioni di primo e secondo grado ottenuti con l'uso delle quattro operazioni elementari e con l'estrazione di radici, anche nel caso che il polinomio P(x) sia completo (cioè contenga tutti i termini dal grado massimo a zero); con l'introduzione dei numeri complessi, possiamo affermare che per tutte le equazioni di primo e secondo grado esistono dei metodi codificati che portano alla loro soluzione (se ne esiste una). Per quelle di grado superiore esistono formule molto complicate per le equazioni di terzo e quarto grado, ma è stata dimostrata l'impossibilità di trovarne una per quelle di grado cinque o superiore.

Non riportiamo i metodi delle soluzioni delle equazioni di 1° e 2° grado perchè noti fin dalle scuole medie inferiori.

Il metodo generale per la risoluzione delle equazioni consiste quindi nella scomposizione del polinomio P(x) in fattori di primo o secondo grado, e nell'applicazione del principio dell'annullamento del prodotto:

Il prodotto di due o più polinomi è nullo se almeno uno di essi è zero.

Tutti gli eventuali valori che rendono vera l'equazione P(x) = 0 si ottengono quindi annullando singolarmente tutti i fattori.

A questa considerazione è legata l'importanza della scomposizione dei polinomi, che abbiamo già esposto nel precedente capitolo e che riassumiamo brevemente qui:

Per la scomposizione di un polinomio in fattori:

1. Contare i termini e mettere a fattore l'eventuale M.C.D. di tutti i suoi termini o raccogliere parzialmente (se conveniente);

2. Riconoscere la potenza di un binomio;

3. Riconoscere la somma o differenza di due potenze con ugual esponente;

4. Applicare il teorema di Ruffini;

La procedura è ricorsiva nel senso che, applicato uno dei metodi soprariportati, si può tentare una successiva scomposizione a ciascun fattore, con gli stessi metodi.

Fra le equazioni che si possono risolvere con questi metodi ricadono quelle

• binomie (v. punto 3) del tipo: xⁿ ± k = 0;

• quelle complete a coefficienti interi, del tipo:

P(x) = a_n xⁿ ± a_n-1 x^n-1 ± .... ± a₀ = 0, con a_n , a_n-1 , a₀ interi,

per le quali è possibile applicare il teorema di Ruffini (v. punto 4) utilizzando come divisore il rapporto ±p/q, ove p è un divisore del termine noto a₀ e q è uno dei divisori del termine di grado massimo a_n.

Notare che se il polinomio è a coefficienti razionali, può essere facilmente trasformato in uno a coefficienti interi, moltiplicando tutti i termini per il m.c.m. fra a₀ e a_n.

Notare inoltre che in tal modo si possono trovare solo le soluzioni razionali x=±p/q.

• quelle reciproche di 3° grado (divisibili per x+1 se di I tipo e per x-1 se di II tipo)

• quelle reciproche di 4° grado (divisibili per x-1 e per x+1, se di II tipo)

come conseguenza del teorema di Ruffini.

Se il polinomio P(x) non è così scomponibile, si può procedere con un altro metodo altrettanto generale:

Si effettua una posizione introducendo una variabile ausiliaria in modo da trasformare l'equazione data in una di primo o secondo grado nella variabile ausiliaria; si risolve poi quest'ultima equazione e si sostituiscono i valori trovati nell'equazione di definizione della variabile ausiliaria.

Facciamo un semplice esempio:

Per risolvere la: (x²+x)² - 6(x²+x) +5 = 0, si ponga: x²+x = t, trasformando l'equazione data in:  t² – 6 t + 5 = 0 e si risolva poi il sistema:

x²+x = t

t² – 6 t + 5 = 0

partendo ovviamente dalla risoluzione delle seconda equazione per determinare i valori di t che saranno sostituiti poi nella prima.

In matematica è sempre possibile effettuare una qualsiasi posizione, che corrisponde in definitiva ad un cambio di nome delle variabili (anche se non sempre conveniente).

Fra le equazioni che si possono risolvere con una posizione ricadono quelle

• biquadratiche del tipo:

a x²ⁿ ± b xⁿ ± c = 0 per le quali basta porre xⁿ = t per trasformarle nel sistema:

xⁿ = t

• quelle reciproche di I tipo e di 4° grado

che si risolvono con la posizione x + 1/x = t, con cui l'equazione: a x⁴- b x³ + c x² - b x + a = 0 si trasforma nel sistema:

poiché, dividendo per x⁴, si ottiene: