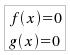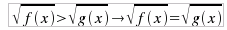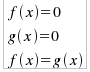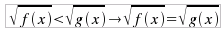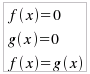|
E' irrazionale una disequazione in cui la variabile compare sotto il segno di radice. I problemi con le disequazioni irrazionali sorgono essenzialmente solo nel caso che l'indice del radicale sia pari, in quanto per gli indici dispari sarebbe sufficiente elevare ambo i membri all'opportuna potenza senza alcuna incertezza sul verso della disequazione: elevare ad una potenza dispari significa infatti moltiplicare il numero per sé stesso un numero pari di volte che è sicuramente positivo, senza problemi per il verso della disequazione. Abbiamo usato il condizionale perchè in effetti elevare ambo i membri ad una stessa potenza equivale ad applicare la seconda proprietà invariantiva che richiede che il fattore per cui si moltiplica sia lo stesso (in valore e segno e diverso da zero) per tutti e due i membri; così non è nel caso delle disequazioni che affermano una sostanziale diversità dei due membri: 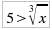 E' quindi sempre necessario considerare la corrispondente equazione: 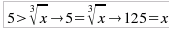 per poter eliminare la radice. Una
volta trovata la soluzione col metodo già indicato nella prima
parte (sulle disequazioni razionali intere o fratte), si dovrà
poi verificare se la disequazione originale è verificata. Una volta trovata la soluzione col metodo già indicato per le disequazioni razionali intere o fratte, si dovrà poi verificare se la disequazione originale è verificata. Perchè moltiplicando per un fattore, si eleva il grado dell'equazione e si aumenta quindi il numero delle soluzioni accettabili.
Ciò vale in tutti i casi del tipo:
con n ed m dispari. Per la risoluzione di un'equazione irrazionale ad indici dispari, per quanto sopra ricordato, conviene scrivere la corrispondente equazione:
valida in tutti e due e casi ed elevare poi ambo i membri alla potenza n-esima (che è dispari) prima e a quella m-esima (che è dispari) poi per ottenere l'equazione equivalente:
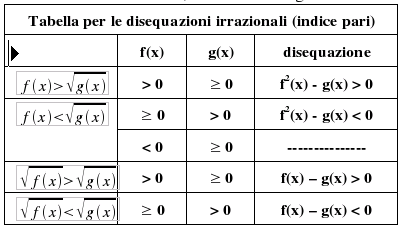
che, essendo razionale, può essere risolta con i metodi delle equazioni intere Per le disequazioni irrazionali ad indice pari bisogna invece imporre sempre la condizione di realtà per tutti i radicali coinvolti e quindi si deve in ogni caso risolvere un sistema di disequazioni: la soluzione sarà rappresentata dall'intersezione degli insiemi di verità di tutte le disequazioni del sistema. Le disequazioni irrazionali ad indice pari sono essenzialmente di 4 tipi distinti:
supponendo, in tutti i casi, che i radicali siano assunti con valore positivo. In ogni caso, per l'osservazione già fatta in precedenza, si dovrà studiare la corrispondente equazione. che si risolve con il sistema:
tradotto nel sistema risolutivo:
per il quale, bisognerà risolvere delle equazioni intere le singole equazioni e, successivamente, calcolare l'intersezione dei rispettivi insiemi di verità (vedere gli esempi allegati). In questo caso si devono considerare due casi distinti a seconda del segno di f(x): II-a: f(x) ≥ 0 che si risolve con il sistema: tradotto nel sistema risolutivo:
per il quale, bisognerà risolvere le singole equazioni con i metodi delle equazioni intere e, successivamente, calcolare l'intersezione dei rispettivi insiemi di verità (perchè le disequazioni devono verificarsi contemporaneamente). oppure: II-b: f(x) < 0 che si risolve con il sistema: (visto
che f(x) < 0 e
per il quale, bisognerà risolvere, con i metodi della I parte, le singole equazioni e, successivamente, calcolare l'intersezione dei rispettivi insiemi di verità (perchè le disequazioni devono verificarsi contemporaneamente). In questo caso non è possibile fare il quadrato di ambo i membri perchè f(x) è negativo. La
soluzione della disequazione sarà poi data dall'unione
degli insiemi di verità dei due casi precedenti. che si risolve con il sistema:  tradotto nel sistema risolutivo:
per il quale, bisognerà risolvere, con i metodi della I parte, le singole equazioni e, successivamente, calcolare l'intersezione dei rispettivi insiemi di verità (perchè le disequazioni devono verificarsi contemporaneamente ).
che si risolve con il sistema:
tradotto nel sistema risolutivo:
per il quale, bisognerà risolvere, con i metodi della I parte, le singole equazioni e, successivamente, calcolare l'intersezione dei rispettivi insiemi di verità (perchè le disequazioni devono verificarsi contemporaneamente). Per
riassumere le diverse situazioni, utilizziamo la seguente tabella:
|
| a inizio
pagina |
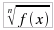 con
n dispari è reale per tutti i valori di f(x).
con
n dispari è reale per tutti i valori di f(x).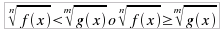
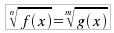
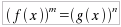
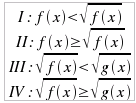
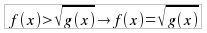
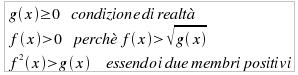
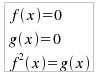
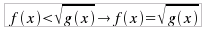

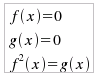

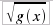 positivo,
non occorre alcuna condizione aggiuntiva), tradotto
nel sistema risolutivo:
positivo,
non occorre alcuna condizione aggiuntiva), tradotto
nel sistema risolutivo: