|
Potenze
con esponente razionale positivo: Si
chiama potenza di base 'a' (
In altri termini:
La funzione non è più a valori discreti in quanto, dato un valore qualsiasi, non è possibile individuarne il successivo, ma il suo codominio è denso poiché tra due valori qualsiasi y1 e y2 tra loro distinti (y1 < y2 ), esistono infiniti altri valori maggiori di y1 e minori di y2.
p e q sono
numeri naturali; q è diverso da 0; se q = 1
Visto che il rapporto
p/q è un numero razionale, i due numeri naturali sono tra loro
commensurabili, esiste cioè un numero m naturale tale
che:
come, ad esempio:
Notiamo che
dall'equivalenza Nel paragrafo dedicato ai radicali, sarà sviluppato un metodo alternativo per il loro calcolo, basato appunto sulle proprietà delle potenze così come già enunciate sopra. |
| a inizio
pagina |

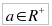 )
ed esponente razionale positivo
(
)
ed esponente razionale positivo
( 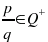 )
quel radicale che ha per indice q e per radicando ap
)
quel radicale che ha per indice q e per radicando ap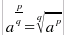
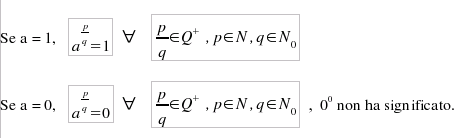
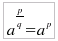
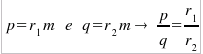
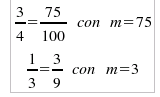
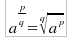 si
deduce che la radice q-esima di a elevato alla p è quel
numero reale r tale che rq = ap e
quindi per i cosiddeti 'radicali' valgono le consuete proprietà
enunciate per le potenze con esponente naturale.
si
deduce che la radice q-esima di a elevato alla p è quel
numero reale r tale che rq = ap e
quindi per i cosiddeti 'radicali' valgono le consuete proprietà
enunciate per le potenze con esponente naturale.