|
Equazioni logaritmiche E' logaritmica un'equazione in cui l'incognita figura come argomento di un logaritmo:
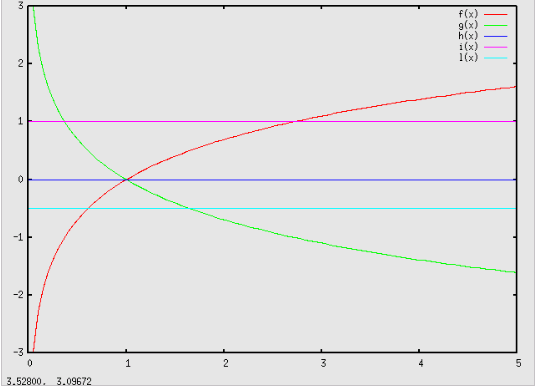
ove f(x) e g(x) sono funzioni polinomiali o semplicemente la variabile x. Dal grafico delle funzioni logaritmiche con base a ∈ R+ (reale positiva), maggiore o minore di 1:
si deduce immediatamente che k/h è un numero reale qualsiasi e che sia nel caso di basi > 1 che in quello di basi minori di 1 (ma sempre maggiori di 0), la soluzione di un'equazione logaritmica è sempre unica. Tutte le equazioni logaritmiche, anche nel caso più complesso, sono risolubili graficamente trovando l'intersezione delle due curve:
In generale le
equazioni
logaritmiche si risolvono applicando ad ambo i membri la sua funzione
inversa (l'esponenziale), in quanto Analogamente al caso delle equazioni esponenziali, anche per quelle logaritmiche, valgono le regole generali:
Nel caso, infine, che le equazioni logaritmiche (P(loga(f(x)) = 0) siano risolubili con una posizione del tipo z = loga(f(x), si dovrà risolvere un sistema costituito dalle due equazioni: z = loga(f(x) P(z) = 0 Ad esempio, per
l'equazione:
z = loga(f(x) m z2+ n z + p = 0 sostituendo i valori
di z
ricavati dalla seconda equazione nella prima. |
| a inizio pagina |

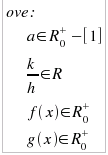
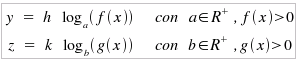
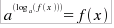
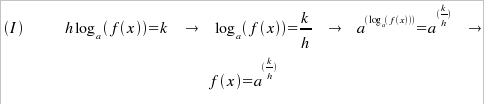
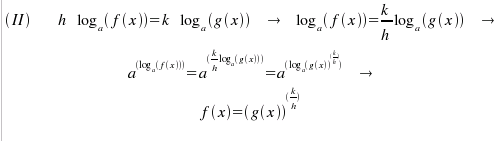
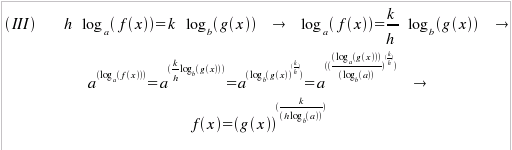
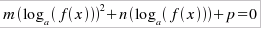 basterà risolvere il
sistema:
basterà risolvere il
sistema: