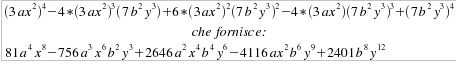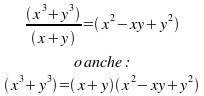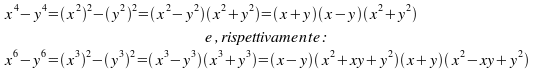|
Alcune immediate condizioni necessarie (ma non sufficienti) per il riconoscimento di una potenza n-sima di un binomio: esistono xn ed yn , con x ed y basi della potenza n-sima di x-y [(x-y)n] o x+y [(x+y)n] il polinomio ha n+1 termini (cioè, ad esempio: (x+y)5 ha 6 termini) Verificate queste semplici condizioni necessarie, controllare che il polinomio contenga tutte le potenze (dalla massima a zero) in tutte e due le basi e che, in aggiunta, i suoi termini siano moltiplicati per i corrispondenti coefficienti del triangolo di Tartaglia (vedere più avanti nel paragrafo). Note: Nei casi più complessi, una volta individuate le due basi, conviene costruire autonomamente la potenza del binomio e verificarne la coincidenza con quello assegnato. Il metodo utilizzato per il riconoscimento è suggerito da quello impiegato per la sua creazione: La potenza n-sima (con n = 2, 3, 4, ...) di un binomio è sempre un polinomio omogeneo di grado n nelle basi (cioè tutti i suoi termini hanno lo stesso grado n complessivo nelle due basi), ordinato secondo le potenze decrescenti della prima base e crescenti della seconda (cioè, nel passaggio da un termine a quello successivo, la prima base diminuisce di un grado mentre la seconda aumenta, sempre di un grado) e completo (cioè contiene tutte le potenze tra la massima n e 0) e ciascun termine è moltiplicato per l'opportuno coefficiente del triangolo di Tartaglia:
In pratica, per costruire la potenza n-sima di un binomio, conviene seguire la procedura seguente (viene riportato un esempio per la potenza (3ax2-7b2y3)4: 1) si scrivano i
termini del polinomio (che dovrà avere n+1 elementi), a
partire dalla potenza n-sima della prima base, diminuendo, per
ogni termine, di 1 grado quello della prima base ed aumentando
di 1 grado quello della seconda, con segni alternati nel caso
(x-y)n e con tutti segni positivi nel caso (x+y)n. (3ax2)4 - (3ax2)3 (7b2y3) + (3ax2)2 (7b2y3)2 - (3ax2) (7b2y3)3 + (7b2y3)4 2) si moltiplichino
i termini per i corrispondenti coefficienti del triangolo di
Tartaglia;
Notare esplicitamente che il polinomio finale, in generale, non è più né omogeneo, né completo... Nei casi più complessi (come nell'esempio riportato), conviene utilizzare la procedura indicata in tutti i suoi passi; solo in quelli molto semplici è consigliabile eseguire direttamente i calcoli.
3.b) Riconoscimento della somma o della differenza di due potenze con ugual esponente. Nota: Vista la comodità e la frequenza negli esercizi applicativi di questi tipi di prodotti notevoli, in presenza di 2 soli termini, conviene sempre verificare che si presenti il caso favorevole, anche quando non è evidente a primo acchito, come nell'esempio: x2-5 che può peraltro essere scritto:
In presenza della somma o differenza di 2 potenze con ugual esponente, risulta molto utile la seguente “tabellinaâ€ン dei prodotti notevoli, che può essere utilizzata sia per l'esecuzione di prodotti notevoli che per la scomposizione in fattori:
In cui, nella prima riga sono riportati i polinomi da dividere per quelli di I grado della prima colonna, mentre nelle caselle centrali è indicato quando la divisione è a resto 0 (cioè quando i due polinomi sono divisibili l'uno per l'altro): ad esempio, “m dispariâ€ン significa che xm + ym è divisibile per (x + y) quando m è dispari; la sequenza dei segni riportati indicano simbolicamente che il polinomio quoziente ha tutti segni positivi (+ + +) o segni alternati (+ - +). L'importanza di questi prodotti notevoli risiede nel fatto che è nota a priori la forma del quoziente costituito sempre da un polinomio omogeneo (di grado n-1 o m-1, a seconda dei casi), ordinato e completo (vedere le definizioni nel paragrafo precedente), del tutto simile a quello delle potenze del binomio, ad eccezione dei coefficienti del triangolo di Tartaglia che, in questo caso, non figurano. Ad esempio:
La stessa tabellina può essere utilizzata anche in senso inverso per trovare immediatamente, nella prima riga, il prodotto del polinomio di primo grado della prima colonna, per uno omogeneo, ordinato e completo con i segni indicati, di grado n-1 o m-1, a seconda dei casi. Ad esempio:
Nota: Nei casi particolari delle differenze di due quarte potenze o di due seste potenze, la scomposizione più favorevole è quella sotto riportata:
che forniscono polinomi di grado inferiore rispetto a quelli che si otterrebbero con la “tabellinaâ€ン di grado 3° e 5°, rispettivamente.
Quando i metodi precedenti non sono sufficienti a scomporre un polinomio in fattori, si può cercare un divisore di primo grado x-a, con a costante, per il polinomio:
(con cn-1, cn-2, ....c0 costanti) in modo tale che sia possibile riscrivere Pn(x) come prodotto di x-a per un opportuno polinomio Pn-1(x) di grado n-1 nella variabile x:
ove le costanti bn-2, bn-3, ...., b0 sono i coefficienti del quoziente Pn(x)/(x-a). Tale ricerca può essere effettuata applicando il teorema di Ruffini: Il polinomio Pn(x), di grado n nella variabile x, con coefficienti cn-1, cn-2, ....c0 costanti, è divisibile per il polinomio di primo grado (x-a), con a costante, se Pn(a) = 0 (cioè se risulta nullo il polinomio Pn(x) quando alla variabile x venga sostituito il valore a). In tal caso dunque: Pn(x) = (x-a) Pn-1(x), ove Pn-1(x) è il polinomio di grado n-1 nella variabile x uguale al quoziente Pn(x)/(x-a). Naturalmente nulla vieta di riapplicare il teorema di Ruffini anche al polinomio Pn-1(x)..... Nota: Il teorema quindi si
applica normalmente verificando se Pn(a) = 0 per
tutti i divisori di c0. Esempio di applicazione del teorema di Ruffini: Trovare un divisore (x-a) del polinomio: x2 - 5x +6 I divisori del numero 6 (termine noto del polinomio) sono: ±6, ±3, ±2, ±1 e la ricerca deve essere effettuata con tutti:
Osservazioni: - La ricerca va fatta con criterio: nel nostro caso, ad esempio, salta agli occhi che tutti i divisori del tipo (x+a) non possono mai portare all'annullamento del polinomio, risultando tutti i termini positivi. - Una volta determinati
n divisori per il polinomio di grado n, è inutile
proseguire perchè sicuramente non ne esistono altri, a
norma del teorema fondamentale dell'algebra. Il teorema di Ruffini è quindi uno strumento che solo nei casi più semplici permette la scomposizione in fattori del polinomio, ma, nonostante ciò, le sue applicazioni pratiche sono molto comuni. 3.d) Scomposizione in fattori mediante la ricerca di soluzioni dell'equazione Pn(x) = 0 Se si possono trovare le soluzioni dell'equazione:
(supponiamo siano x1, x2, x3, ...., xn), per definizione si ha che:
In definitiva, per scomporre un polinomio qualsiasi di grado n Pn(x), è sempre possibile ricercare le soluzioni della corrispondente equazione Pn(x) = 0 e, in caso positivo, riscrivere il polinomio come prodotto di più fattori
se x1, x2, x3, ...., xn sono le n soluzioni trovate. Ovviamente, non è necessario trovare tutte le soluzioni x1, x2, x3, ...., xn per poter scrivere:
se x1, x2 soluzioni e Pn-2(x) polinomio di grado n-2. Dalle considerazioni fatte si ricava facilmente il seguente Metodo ricorsivo per la semplificazione delle espressioni algebriche:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||