Trigonometria.

Teorema del coseno (Carnot)

Per dimostrare il teorema del coseno, valido per triangoli qualunque, è necessario considerare due casi distinti a seconda che l'angolo compreso tra i due lati sia minore o maggiore di π/2:

Caso dell'angolo α < π/2

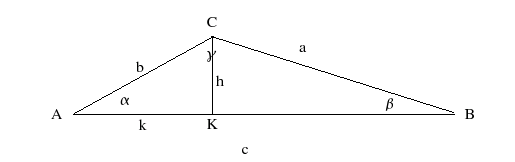Considerando il triangolo CKA, si ha che: h = b sin(α) e k = b cos(α)

Applicando ora il teorema di Piatgora al triangolo CKB, sono verificate le seguenti uguaglianze:

a² = h² + (c-k)² = h² + c² + k² -2ck = b² sin²(α) + b² cos²(α) + c² – 2bc cos(α) =

= b² + c² – 2bc cos(α)

Caso dell'angolo α > π/2

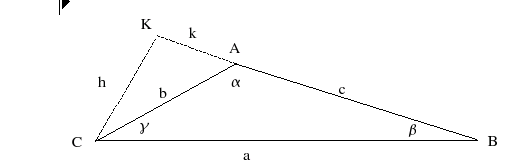Considerando il triangolo CKA, si ha che: h = b sin(π - α) = b sin(α) e

k = b cos(π - α) = b cos(α)

Applicando ora il teorema di Piatgora al triangolo CKB, sono verificate le seguenti uguaglianze:

a² = h² + (c+k)² = h² + c² + k² +2ck = b² sin²(α) + b² cos²(α) + c² – 2bc cos(α) = b² + c² – 2bc cos(α)

E quindi possiamo enunciare il teorema del coseno (o di Carnot):

In un triangolo qualunque il quadrato costruito su un lato è equivalente alla somma dei quadrati costruiti sugli altri due diminuita del doppio prodotto di questi per il coseno dell'angolo tra essi compreso:

a² = b² + c² – 2bc cos(α)