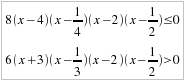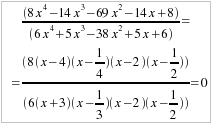Esempio n. 1 (col metodo tradizionale)Risolvere
la disequazione fratta:
Applicando la I prop. Invariantiva:
A questo punto viene applicata la II prop. Invariantiva senza tener conto che il prodotto (x+2)*(x-2) potrebbe essere negativo per alcuni valori di x e che quindi potrebbe cambiare il verso della disequazione, trasformandola nella seguente:
che equivale a risolvere i due sistemi di disequazioni seguenti: 5x-2 > 0 5x-2 < 0 e x2-4 > 0 x2 -4 < 0 Il primo sistema è risolto dall'intersezione degli insiemi di verità delle due disequazioni: (5x-2) > 0 ------------------------------------[2/5]************************************************************* (x2-4) > 0 ********[-2#]--------------------------------------------------------[2#]****************************** che equivale a: ----------------------------------------------------------------------[2]************************ con soluzione x > 2. Il secondo sistema è risolto dall'intersezione degli insiemi di verità delle due disequazioni: (5x-2) < 0 ********************************[2/5]-------------------------------------------------------------------- (x2-4) < 0 ----------[-2#]*************************************[2#]-------------------------------------------------- che equivale a: ----------[-2#]***************[2/5]--------------------------------------------------------------------- con soluzione -2 < x < 2/5. Con il concelletto # abbiamo indicato i punti singolari, mentre con * gli intervalli in cui è verificata la corrispondente disequazione. Quindi, con l'unione dei due insiemi di verità, si ha, come soluzione della disequazione, l'insieme: ] -2, 2/5 [ ∪ ] 2, + ∞ [ Esempio n. 1 (col metodo innovativo)Applicando la I prop. Invariantiva:
Si scrive ora la corrispondente equazione a cui è possibile applicare anche la II prop. Invariantiva e si ottiene:
Si moltiplica il numeratore per il denominatore, facendo peraltro notare che quest'ultimo deve essere diverso da zero (cosa trascurata nel metodo precedente), ottenendo il seguente sistema: (5x-2)(x2-4)
= 0 Si riportano su un unico grafico tutte le soluzioni delle due equazioni: 5x-2 = 0, con soluzione x = 2/5 e x2-4 = 0, con soluzioni x = ± 2 e si assegnano i segni ai tre intervalli, partendo da quello ]2, +∞[ in cui il polinomio è positivo (perchè tale è il segno di 5x*x2). In definitiva la disequazione è soddisfatta in tutti gli intervalli indicati con il segno + : - + - + ---------------------[-2#]-------------------------------[2/5]----------------------------------------[2#]--------------------------- e cioè in ]-2,2/5[ e in ] 2, +∞ [ Esempio n. 2 (col metodo tradizionale)Risolvere
la disequazione:
Scomponiamo in fattori numeratore e denominatore, ottenendo la:
che equivale a risolvere i due sistemi di disequazioni seguenti:
Il primo sistema si risolve imponendo che sia la prima che la seconda equazione assumano valori positivi, risolvendo quindi i sistemi di equazioni: I-1
] - ∞ , 0[ ∪ ]2, + ∞ [
Dunque la seconda equazione del primo sistema è soddisfatta dall'unione degli intervalli: ] - ∞ , -1[ ∪ ]1, + ∞ [ Notiamo esplicitamente che i punti -1 e 1 devono essere esclusi perchè singolari per il rapporto considerato. Infine (ma non è ancora finito....) il primo sistema è soddisfatto dall'intersezione dei due insiemi di verità delle due disequazioni che lo compongono: 2x(x-2)(x2+2x+4) > 0 *********************************[0]--------------[2]************************* (x2+1)(x+1)(x-1) > 0 *************************[-1]---------------[1]******************************* e cioè dall'insieme di verità: *************************[-1]----------------------[2]*************************** corrispondente all'unione dei due intervalli: ] - ∞ , -1[ ∪ ]2, + ∞ [ Teoricamente bisognerebbe ripetere la stessa procedura per il secondo sistema (che ovviamente qui non riporteremo...), ottenendo per esso l'insieme di verità complessivo: ] 0,1 [ La soluzione della disequazione sarebbe quindi fornita dall'unione dei due insiemi di verità ricavati dai due sistemi:
corrispondente all'unione degli intervalli: ] - ∞ , -1[ ∪ ] 0, 1 [ ∪ ] 2, + ∞ [
Per fortuna esiste un metodo alternativo a questo....
Esempio n. 2 (col metodo innovativo)Risolvere
la disequazione:
Scomponiamo in fattori numeratore e denominatore, ottenendo la:
Moltiplichiamo numeratore per denominatore e risolviamo la corrispondente equazione, rammentando che il denominatore deve essere diverso da zero: 2x (x-2) (x2+2x+4) (x2+1) (x+1) (x-1) = 0 (x2+1) (x+1) (x-1) ≠ 0 Risolviamo dunque le singole equazioni, applicando il principio di annullamento del prodotto:
Riportiamo su un unico grafico tutte le soluzioni reali e assegniamo i segni agli intervalli, partendo da quello ]2, +∞[ in cui il polinomio è positivo (perchè tale è il segno di 2x*x*x2*x2*x*x). In definitiva la disequazione è soddisfatta in tutti gli intervalli indicati con il segno +: + - + - + ***************[-1#]---------[0]********[1#]--------[2]*************************************** con lo stesso insieme di verità trovato con l'altro metodo, ma con una procedura certamente più semplice.... Esempio n. 3 (col metodo tradizionale)Risolvere
la disequazione:
Scomponiamo in fattori numeratore e denominatore, ottenendo la:
La disequazione ha significato per x ≠ -3, x ≠ 1/3, x ≠ 2 e x ≠ ½. Ci potrebbe venire in mente di semplificare l'espressione -dividendo numeratore e denominatore per (x—2)(x-1/2)- ma ciò non è lecito perchè non si sa se i due fattori sono diversi da zero e, per di più, per la disequazione, non conosciamo il segno dei fattori, anche se tale operazione non comporterebbe la modifica del segno!! La semplificazione produrrebbe comunque, in questo caso, anche la sparizione di due radici dall'insieme degli zeri dei polinomi. Riteniamo dunque che il metodo tradizionale, molto complicato come vedremo in seguito, può creare problemi e generare errori nel computo degli insiemi di verità (soprattutto nel caso di disequazioni in senso lato, cioè con le relazioni ≤ o ≥ ). A questo punto dovremmo risolvere i soliti due sistemi costituiti dalle disequazioni:
costituiti, ciascuno, da ben 8 disequazioni:
|
|
|
|
|
| Per risolvere il sistema è sufficiente moltiplicare i segni in tutti gli intervalli individuati dal simbolo “|” e verificare quando i loro prodotti siano negativi o nulli, ottenendo gli insiemi di verità: ]-3, ¼] ∪ ]1/3, ½[ ∪ ]½,2[ ∪ ]2,4] poiché, in tali intervalli, il prodotto dei segni è negativo. Notare che i punti singolari -3, 1/3, 1/2, 2, contrassegnati dal cancelletto # , sono stati esclusi. Utilizzeremo ora il metodo alternativo per dimostrare quanto sia di più semplice applicazione. Esempio n. 3 (col metodo innovativo)Risolvere
la disequazione:
Come col metodo tradizionale, scomponiamo in fattori numeratore e denominatore, e riscriviamo la corrispondente equazione, ottenendo la:
moltiplichiamo ora il numeratore per il denominatore e scriviamo il sistema risolvente:
Riportiamo su un unico grafico tutte le soluzioni indicando quelle di molteplicità dispari con le coppie di parentesi quadre [ ] e quelle di molteplicità pari con le tonde ( ) ed evidenziando quelle da escludere col il cancelletto # : + - + - - - + -----[-3#]---------------[1/4]---------[1/3#]----------(1/2#)------------------(2#)--------------------[4]------------------------ ove i segni sono stati stabiliti a partire dall'ultimo intervallo [4,+∞ [ caratterizzato da un segno positivo perchè tale è il prodotto dei termini dominanti di tutti i fattori: x*x*x2*x2*x*x Otteniamo così, più facilmente, l'insieme di verità della disequazione: ]-3,1/4] ∪ ]1/3, ½ [ ∪ ]1/2,2[ ∪ ]2,4] con esclusione dei punti singolari -3, 1/3, 1/2, 2 che annullerebbero il denominatore. |
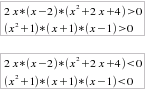
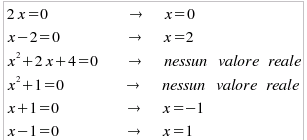
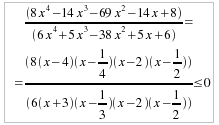
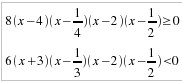 e
e