|
Potenza
con esponente reale (o esponenziale in base a): L'estensione alle potenze con esponente irrazionale (e quindi a quelle con esponente reale) pone un problema in quanto il numero irrazionale (con infinite cifre decimali non periodiche) è individuato da due classi contigue di numeri razionali, caratterizzate dalla proprietà che ogni numero della prima classe è minore di ciascuno dei numeri della seconda classe e che, comunque piccolo si fissi un numero , esistono sempre due numeri appartenenti alle due classi tali che la loro differenza sia in modulo minore di . In altre parole, le due classi di numeri approssimano quanto si vuole il numero irrazionale con valori per eccesso e per difetto ed individuano in tal modo, in maniera univoca, il numero irrazionale stesso come elemento separatore delle due classi. Utilizzando questa proprietà è possibile definire due classi contigue di potenze con esponenti razionali individuati dai numeri delle due classi che hanno come elemento separatore l'esponente reale.
Così la potenza
che godono delle due proprietà
sopra ricordate e che quindi individuano come loro elemento di
separazione unico la potenza Si
chiama potenza di base 'a' ( Quando x ∈N, y = ax è una potenza reale ad esponente naturale; Quando x ∈Q, y = ax è una potenza reale ad esponente razionale; Quando a = 0, y = ax è la funzione costante y=0. Quando a = 1, y = ax è la funzione costante y=1.
E' una funzione continua (cioè non discreta come
accadeva per esponenti naturali o interi, poiché x ∈
R+) definita per tutti i valori reali di x e per ogni
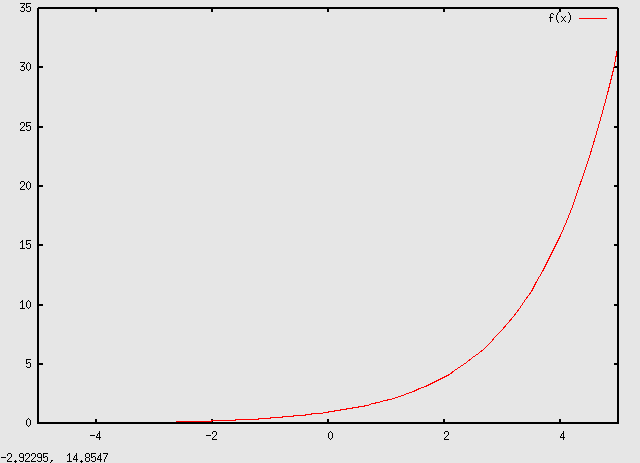
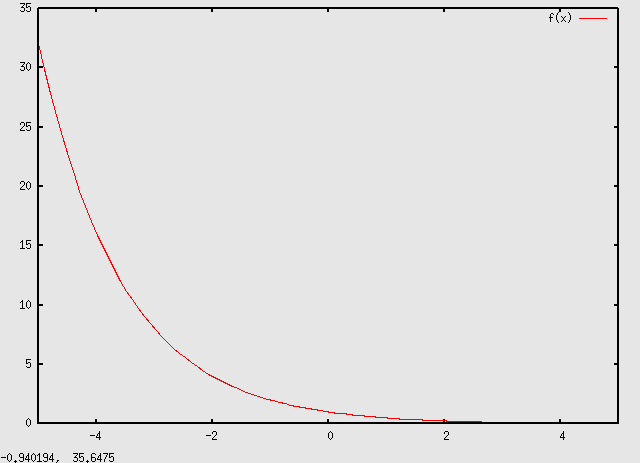
valore reale positivo della base ( Per la funzione y = ax valgono le consuete proprietà già ricordate all'inizio per le potenze ad esponente naturale. Possiamo rappresentare la funzione esponenziale y = ax nei due casi distinti che a, sempre positivo, sia maggiore di 1 oppure compreso tra 0 ed 1:
Per a = 1, la funzione y = ax assume ovviamente sempre il valore 1.
Le proprietà della funzione esponenziale e della sua inversa
(funzione logaritmo) sono descritte nella sezione ad esse dedicata
(Funzioni esponenziali e logaritmiche). |
||||
| a inizio
pagina |

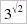 sarà
individuata dalle due classi contigue:
sarà
individuata dalle due classi contigue:

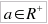 )
ed esponente reale x (
)
ed esponente reale x (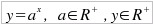 )
quel numero reale coincidente con l'elemento separatore delle due
classi contigue di numeri reali che si ottengono elevando la base ai
valori approssimati rispettivamente per eccesso e per difetto che
individuano l'esponente reale x.
)
quel numero reale coincidente con l'elemento separatore delle due
classi contigue di numeri reali che si ottengono elevando la base ai
valori approssimati rispettivamente per eccesso e per difetto che
individuano l'esponente reale x.