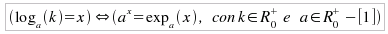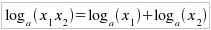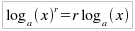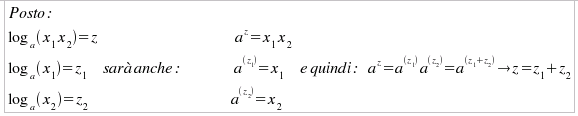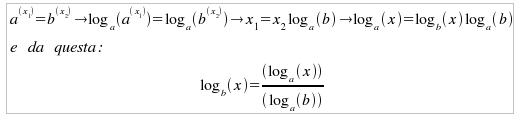|
Funzioni logaritmiche La funzione esponenziale y = ax è invertibile, cioè esiste la sua funzione inversa (che chiameremo funzione logaritmica o semplicemente logaritmo):
Definizione: Si chiama logaritmo di un numero k ∈ R0+ (reale positivo) in una prefissata base a ∈ R0+ -{1} (reale positiva e diversa da 1), l'esponente x al quale si deve elevare la base a per ottenere il numero k. In altre parole il logaritmo di un numero k ∈ R0+ si presenta come soluzione x dell'equazione esponenziale k = ax.
Proprietà della funzione logaritmica y = loga(x) Come conseguenza immediata della definizione, sussiste l'uguaglianza:
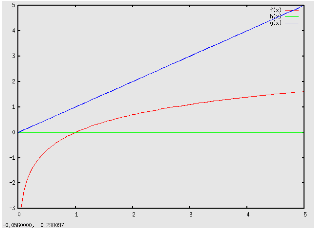
Dalla definizione di funzione inversa, si deduce immediatamente che: loga(expa(x)) = x e che: expa(loga(x)) = x Ancora, dalle proprietà delle funzioni inverse, alla coppia di coordinate (x,y) della curva esponenziale nella base a, corrisponde la coppia di coordinate (y,x) di quella logaritmica nella stessa base e quindi il grafico di loga(y) è la curva simmetrica di quella expa(x) rispetto alla bisettrice del I e III quadrante:
Dalla rappresentazione grafica di si deduce facilmente che:
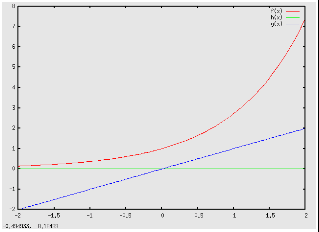
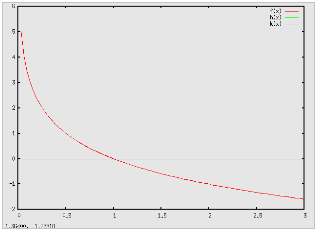
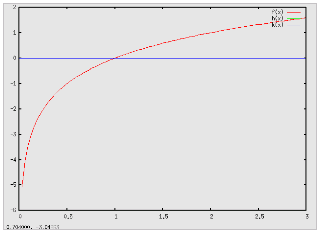
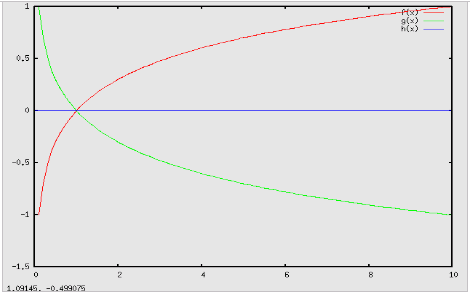
Il loga(x) è definito soltanto per valori positivi dell'argomento x, essendo soluzione della corrispondente equazioni esponenziale. Nel caso che la base a sia positiva, ma minore di 1: Il loga(x) è strettamente decrescente Il loga(x) è negativo se x > 1 Il loga(x) è positivo se 0 < x < 1 Nel caso che la base a sia maggiore di 1: Il loga(x) è strettamente crescente Il loga(x) è positivo se x > 1 Il loga(x) è negativo se 0 < x < 1 L'asse delle ordinate è asintoto verticale per x → 0, qualunque sia la base positiva a. Il loga(1) = 0, qualunque sia la base positiva a. A parità di variazione di x, la velocità di variazione di y = loga(x) è tanto più grande quanto maggiore è la base a, se a > 1 e tanto più piccola quanto minore è la base a, se 0 < a <1. Funzioni logaritmiche di basi una inversa dell'altra sono simmetriche rispettoall'asse delle ascisse, cioè assumono lo stesso valore per valori opposti dell'argomento. Nelle applicazioni che coinvolgono funzioni logaritmiche è sempre opportuno far riferimento mnemonico alla rappresentazione grafica dei due tipi (per a >1 o per a < 1):
L'uso della funzione logaritmica è giustificato dalla presenza di tale funzione in molte leggi della fisica e di altre scienze, perchè tali funzioni descrivono fenomeni che si evolvono molto lentamente nel tempo (come, ad esempio, il decadimento radioattivo), ma anche da alcune importanti proprietà che, prima dell'avvento delle macchine calcolatrici e dei computer, permettevano l'esecuzione di calcoli complicati, impensabili con altre metodologie. Riportiamo di seguito alcuni teoremi sui logaritmi che illustrano l'uso di tali funzioni per il calcolo: Teorema del prodotto:
Il logaritmo del prodotto di due fattori positivi è
uguale alla somma dei logaritmi dei singoli fattori:
Teorema del quoziente:
Il logaritmo del quoziente di due fattori positivi è
uguale alla differenza dei logaritmi dei singoli fattori: 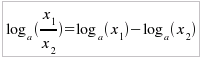 Teorema della potenza e della radice:
Il logaritmo della potenza (intera o reale) di un numero
positivo è uguale al prodotto dell'esponete per il logaritmo
del numero: Le dimostrazioni sono immediate in base alla definizione della funzione:
Le altre dimostrazioni sono analoghe. Una importante proprietà dei logaritmi ci permette di passare da un logaritmo in una base ad uno espresso mediante un'altra: supponiamo di conoscere il logaritmo di uno stesso numero x in due basi differenti e sia x1 = loga(x) e x2=logb(x), allora per definizione si verifica che:
|
||||||||
| a inizio
pagina |