|
Per definizione, si ha:
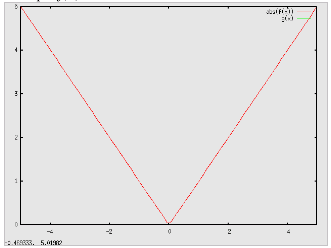
e quindi la rappresentazione grafica del valore assoluto di f(x) è la seguente: per una funzione lineare del tipo f(x) = x:
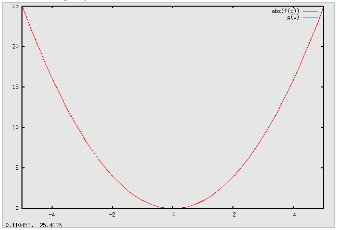
per una funzione quadratica del tipo f(x) = x2:
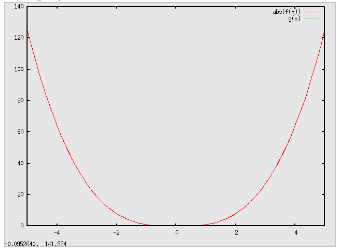
per una funzione cubica del tipo f(x) = x3:
La funzione dunque non assume mai valori negativi. Pertanto
il confronto del
valore
assoluto di una funzione f(x) con una costante negativa o è
sempre verificato (
Il confronto di |f(x)| con una costante positiva o nulla dipende sia dal verso della disequazione che dal valore della costante. Prima
di sviluppare la teoria relativa, a scopo esemplificativo,
rappresentiamo graficamente la situazione nel caso che
Nei
tre casi, gli insiemi di verità in cui si verifica che Caso k = k1 = 2: Per definizione, si deve risolvere il sistema costituito dalle due disequazioni:
 e
quindi con l'insieme di verità costituito dall'unione dei due
intervalli in cui sono contemporameamente soddisfatte le due
disequazioni:  Caso k = k2 = 4: Per definizione, si deve risolvere il sistema costituito dalle due disequazioni:
 e
quindi con l'insieme di verità costituito dall'unione dei due
intervalli in cui sono contemporameamente soddisfatte le due
disequazioni: 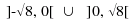 Caso k = k3 = 7: Per definizione, si deve risolvere il sistema costituito dalle due disequazioni:
 e
quindi con l'insieme di verità costituito dall'unico
intervallo in cui sono contemporameamente soddisfatte le due
disequazioni: 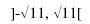 Il procedimento adottato per la funzione quadratica f(x) = |x2-4| può essere utilizzato per qualsiasi altra funzione. Nel caso che la disequazione sia del tipo |x2-4| > k, con k >= 0, la rappresentazione grafica sarà la stessa già utilizzata nel caso precedente, ma gli insiemi di verità non saranno più costituiti dagli intervalli soluzioni di un sistema (e cioè dalla intersezione degli insiemi di verità delle due disequazioni), ma dalla loro unione. Riprendendo i tre casi precedenti, si ha: Caso k = k1 = 2: Come già ricordato, si devono risolvere le due disequazioni, che NON costituiscono sistema:
 e
quindi con l'insieme di verità costituito dall'unione dei due
intervalli in cui sono soddisfatte separatamente le due
disequazioni: Caso k = k2 = 4: Si devono risolvere le due disequazioni, che NON costituiscono sistema:
( Caso k = k3 = 7: Si devono risolvere le due disequazioni, che NON costituiscono sistema:
(
Bisogna dunque fare molta attenzione alla differenza sostanziale nei due casi esaminati, ricordando che con la disequazione del tipo |f(x)| < k, con k >= 0, si deve risolvere un sistema, mentre con la disequazione della forma |f(x)| > k, con k >= 0, le due disequazioni sono tra loro indipendenti. Per continuare nella esemplificazione grafica, quando alla costante k sia sostituita una funzione g(x), cioè per la disequazione del tipo: |f(x)| >= g(x) oppure |f(x)| < g(x) , mentre il procedimento rimane inalterato, bisognerà, caso per caso, stabilire il segno della funzione g(x) prima di adottare uno dei due procedimenti, infatti: per ogni x tale che g(x) >= 0
per ogni x tale che g(x) < 0
La rappresentazione grafica del problema nel caso che le funzioni siano: f(x) = x2-6, g1(x) = x2+1, g2(x) = x2-1, g3(x) = x2+8, è quella riportata in figura:
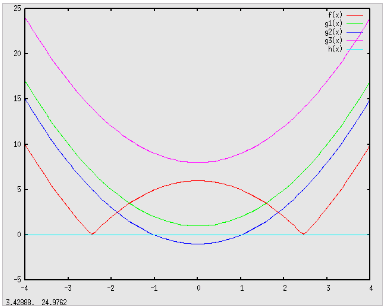 Tratteremo ora il problema in generale, e quindi nel caso |f(x)| < g(x) e in quello |f(x)| >= g(x), intendendo che la funzione g(x) può anche essere costante positiva, nulla o negativa. Analizziamo dapprima la: |f(x)| < g(x) si possono verificare due casi distinti: a) g(x) <= 0 ⇒ la disequazione non è mai soddisfatta (ovviamente per tutti gli x appartenenti al dominio di negatività di g(x)); b) g(x) > 0 ⇒ la disequazione è soddisfatta dalle soluzioni del sistema costituito dalle due disequazioni, e quindi dall'intersezione dei loro insiemi di verità: f(x) < g(x), per ogni x tale che f(x) >= 0, per ogni x tale che g(x) > 0 |f(x)| < g(x) ⇔ f(x) > - g(x), per ogni x tale che f(x) < 0, per ogni x tale che g(x) > 0 Passiamo ora alla: |f(x)| > g(x) ancora una volta si possono distinguere due casi distinti: c) g(x) <= 0 ⇒ la disequazione non è sempre soddisfatta (ovviamente per tutti gli x appartenenti al dominio di negatività di g(x)); b) g(x) > 0 ⇒ la disequazione è soddisfatta dalle soluzioni delle due disequazioni (che NON costituiscono sistema) e quindi dall'unione dei loro insiemi di verità: f(x) > g(x), per ogni x tale che f(x) >= 0, per ogni x tale che g(x) > 0 |f(x)| > g(x) ⇔ f(x) < - g(x), per ogni x tale che f(x) < 0, per ogni x tale che g(x) > 0 La situazione è schematizzata sinteticamente nella seguente tabella:
In definitva, il procedimento pratico per la risoluzione di una disequazione che contenga un valore assoluto, |f(x)| >= g(x) oppure |f(x)| < g(x), implica dapprima la determinazione del segno di g(x) (banale nel caso che g(x) sia una costante) e, nel caso non si sappia già a priori che la disequazione non è MAI o è SEMPRE soddisfatta,
|
||||||||||||
| a inizio pagina | ||||||||||||
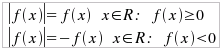
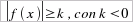 ) o non lo
è in
nessun caso (
) o non lo
è in
nessun caso (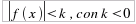 ).
).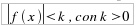 per
la funzione quadratica f(x) = x2 - 4 e per 3 valori
diversi di k (k1 = 2 , k2 = 4 , k3 =
7 ):
per
la funzione quadratica f(x) = x2 - 4 e per 3 valori
diversi di k (k1 = 2 , k2 = 4 , k3 =
7 ):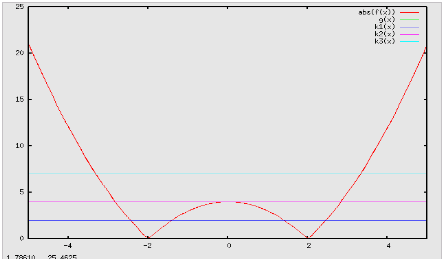
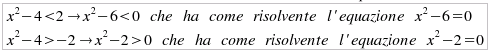
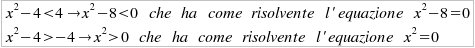
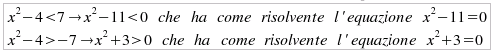
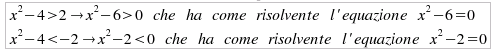
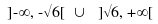 per la prima
e
per la prima
e 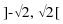 per la seconda.
per la seconda.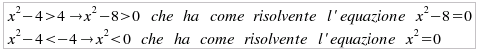

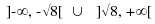 ) poichè la seconda
ha come insieme di verità l'insieme vuoto ∅.
) poichè la seconda
ha come insieme di verità l'insieme vuoto ∅.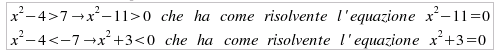

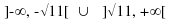 ) poichè la seconda
ha come insieme di verità l'insieme vuoto ∅.
) poichè la seconda
ha come insieme di verità l'insieme vuoto ∅.