|
I) Studio della disequazione |x| < 8 Dalla prima riga della tabella, visto che g(x) = 8 è certamente positivo, si passa direttamente a risolvere il sistema di disequazioni:
 con un insieme di verità dato dall'intersezione di quello della prima disequazione ]-∞,8[ con quello della seconda ]-8,+∞[, cioè dall'intervallo ]-8,8[ in cui sono soddisfatte contemporaneamente le due disequazioni. II) Studio della disequazione |x2+2x-10| < 5 (analogo al precedente) Dalla prima riga della tabella, visto che g(x) = 5 è certamente positivo, si passa direttamente a risolvere il sistema di disequazioni:
 con un insieme di verità dato dall'intersezione di quello della prima disequazione ]-∞,-1-√6[ ∪ ]-1+√6,+∞[ (indicato dal segno ⊕ nel grafico), con quello della seconda ]-5,3[ (indicato dal segno ⊖ nel grafico) e cioè negli intervalli ] -5, -1-√6 [ ∪ ]-1+√6, 3[ in cui sono soddisfatte contemporaneamente le due disequazioni. III)
Studio della disequazione |x|
> 5

con un insieme di verità
dato dall'unione di quello della prima disequazione
]5, +∞[ con quello della
seconda ]-∞ ,-5[ Dalla seconda riga della tabella, visto che g(x) = 6 è certamente positivo, si passa direttamente a risolvere le due disequazioni (che, in questo caso, NON costituiscono sistema, per cui dovremo considerare l'unione degli intervalli di verità delle due disequazioni):
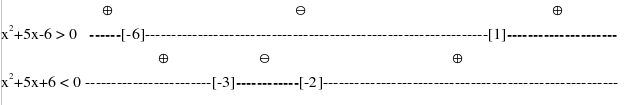 con un insieme di verità dato dalla unione di quello della prima disequazione ]-∞,-6[ ∪ ]1,+∞[ (indicato dal segno ⊕ nel grafico), uniti a loro volta con quello della seconda ]-3,-2[ (indicato dal segno ⊖ nel grafico). L'insieme di verità complessivo è dato dunque da: ]-∞,-6[ ∪ ]1,+∞[ ∪ ]-3,-2[ V) Studio della disequazione |x| > -8 Dalla seconda riga della tabella, visto che g(x) = -8 è certamente negativo, si si deduce che la disequazione è sempre soddisfatta, qualunque sia il valore reale di x. La disequazione |f(x)| > -8 è soddisfatta in tutto il dominio di f(x).
Dalla prima riga della tabella, visto che g(x) = -8 è certamente negativo, si si deduce che la disequazione non è mai soddisfatta, qualunque sia il valore reale di x. La disequazione |f(x)| < -4 non è mai soddisfatta in tutto il dominio di f(x). VII) Studio della disequazione: |3x2 -2x + 1| > 5x2 – 10x -5
 e
negativo per: 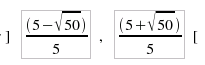 2)
Dalla seconda riga della tabella si deduce immediatamente che la
disequazione è sempre soddisfatta per x nell'intervallo: 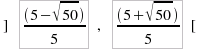 perchè in tale intervallo g(x) risulta negativo, ad esclusione dei punti in cui f(x) = 3x2 -2x + 1 = 0. 3) Per gli altri due intervalli, in cui g(x) risulta strettamente positivo, si dovranno risolvere le due disequazioni seguenti (che NON costituiscono sistema e che quindi forniranno come soluzione la unione dei rispettivi insiemi di verità):
 Le prime due disequazioni si possono considerare solo all'interno degli intervalli: ]-∞,x5[ e ]x6, +∞ [ in cui g(x) = 5x2 – 10x -5 è positiva. In conclusione, l'insieme di verità complessivo della disequazione |3x2 -2x + 1| > 5x2 – 10x -5 è il seguente: ]x1,x5[
∪
]x6,x2[ ove è soddisfatta la prima disequazione, mentre la seconda non è mai soddisfatta all'interno dell'intervallo in cui g(x) è positiva. VIII) Studio della disequazione: |3x2 -2x + 1| < 5x2 – 10x -5
3)
Per gli altri due intervalli, in cui g(x) risulta strettamente
positivo, si dovrà risolvere il sistema delle due
disequazioni seguenti (con un insieme di verità fornito
dall'intersezione di quelli delle due disequazioni): 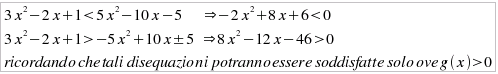
In questo caso, pur essendo luguali le soluzioni delle equazioni corrsipondenti, cambiano gli insiemi di verità, perchè sono opposti i versi: 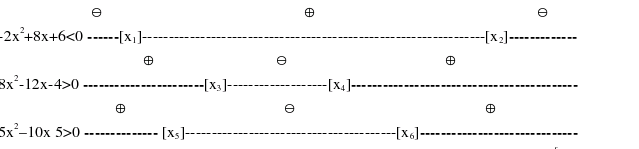 La prima disequazione è soddisfatta nell'intervallo ] -∞, x1 [ e nell'intervallo ] x2, +∞ [ e la seconda nell'intervallo ] -∞, x3 [ e nell'intervallo ] x4, +∞ [; In conclusione, l'insieme di verità complessivo della disequazione |3x2 -2x + 1| < 5x2 – 10x -5 è il seguente: ] -∞, x1 [ ∪ ] x2, +∞ [ che fornisce l'intersezione degli insiemi di verità delle tre disequazioni: -2x2 + 8x + 6 < 0 8x2-12x - 4 > 0 5x2–10x
– 5 > 0
|
| a inizio pagina |
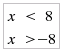 che
corrisponde al sistema risolvente:
che
corrisponde al sistema risolvente: 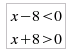
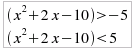 che
corrisponde al sistema
che
corrisponde al sistema 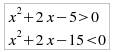
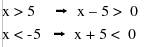
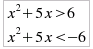 equivalenti a
equivalenti a 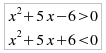 che
portano agli insiemi di verità:
che
portano agli insiemi di verità: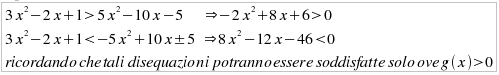
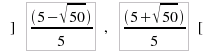 ] perchè in tale
intervallo g(x) risulta negativo.
] perchè in tale
intervallo g(x) risulta negativo.