|
Risoluzione di equazioni
del tipo sin(f(x)) = m e analoghe Per comodità del 'lettore', riportiamo di seguito alcuni valori delle tre funzioni per angoli che frequentemente si incontrano negli esercizi assegnati in classe e per i rispettivi periodi: Valori del seno dell'angolo: Valori del coseno dell'angolo: Valori della tangente dell'angolo: I
due
metodi grafici sopra utilizzati servono a risolvere le equazioni
goniometriche nei casi che capitano più frequentemente,
cioè
quando m corrisponde ad un valore noto della funzione considerata; in
caso diverso, si dovrà ricorrere alle tavole dei valori delle
funzioni goniometriche o all'uso di una calcolatrice o di un
computer, ma in ogni caso, hanno il pregio notevole di individuare tutte le possibili
soluzioni all'interno del periodo; senza la
rappresentazione grafica, capita spesso infatti di 'dimenticare'
qualche soluzione (trascurando così una infinità di
valori..). Ad esempio, l'equazione sin(y) = 0,5 ha certamente come
soluzione y = π/4, ma ha anche
3 / 4 π , che viene spesso
dimenticata. y1 ± 2k π , con k=0,1,2,3,...
e y2 ±
2k π , con k=0,1,2,3,...
Analogamente
per l'equazione cos(y) = m. y1 ± k π , con k=0,1,2,3,...
se y1
è la soluzione trovata all'interno del periodo
e
che
la funzione ha come punti singolari in cui non è definita,
tutti i valori di x = π/2
± kπ.
sin(3x-5)
= 0,5
Si faccia
la
posizione y =
3x-5 e si risolva il sistema: y
= 3x-5
Partendo
dalla
seconda
equazione, si ottiene facilmente: sin(y) = 0,5 y1 = 1 / 4 π
± 2k π , con
k=0,1,2,3,... e y2 = 3 / 4 π
± 2k π , con
k=0,1,2,3,...
A
questo punto, per determinare i valori richiesti di x, si
sostituiscano nella prima equazione del sistema ottenendo le
soluzioni: 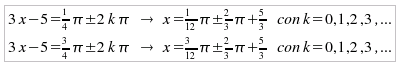 |


