Matematica per tutti
Suggerimenti, proposte, opinioni... per la
didattica della Matematica
Inviate le vostre
proposte,
commenti, obiezioni ... a
Giorgio Lironcurti: giorgio.lir@virgilio.it
|
Risoluzione di equazioni omogenee e non, in più funzioni Nel caso che le funzioni con cui è espressa l'equazione siano tra loro diverse, ma l'equazione sia omogenea (cioè senza termine noto), si dovrà In alternativa
è possibile utilizzare un metodo grafico, come nell'esempio in
cui si suppone di
risolvere la sin(2x) = cos(2x):  Nel caso che le due funzioni siano cos(f(x)) e sin(f(x)), è possibile dividere ambo i membri per il coseno, escludendo però tutti i valori degli angoli che annullano il cos(f(x)): x ≠π/2∓ kπ) che sono punti in cui il polinomio cambia di segno. equazione del tipo: a sin(x) + b cos(x) = 0 Dividere ambo i membri per cos(x), escludendo i valori di x per cui cos(x) = 0, per ottenere la:
a tan(x) + b = 0, con x ≠ π/2±kπ
che si risolve con il
sistema:
y = tan(x)
equazione del tipo: a sin2(x) + b
sin(x)cos(x) +c
cos2(x) = 0 a y + b = 0 cos(x) ≠ 0 Dividere ambo i membri per cos2(x), escludendo i valori di x per cui cos(x) = 0, per ottenere la: a tan2(x) + b tan(x) + c = 0, con x ≠ π/2±kπ che si risolve con il sistema: y = tan(x)
cos(x) ≠ 0 a y2 + b y + c = 0 equazione del tipo: a sin(x) + b cos(x) + c = 0 (non omogenea di 1° grado): Utilizzare la trasformazione 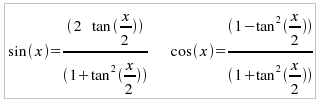
y = tan(x/2)
con x/2 ≠
π/2±kπ (c-b) y2 + 2a y + b + c = 0 equazione del tipo: a sin2(x) + b sin(x)cos(x) +c cos2(x) + d = 0 (non omogenea di 2° grado): Moltiplicare il termine noto per: cos2(x)+sin2(x), che è uguale ad 1, e raccogliere a fattor comune: (a+d) sin2(x) + b sin(x)cos(x) + (c+d) cos2(x) = 0 dividere quindi per cos2(x), con x ≠ π/2±kπ, ottenendo la: (a+d) tan2(x) + b tan(x) + (c+d) = 0 che si risolve col sistema: y = tan(x) (a+d) y2 + b y + (c+d) = 0 con x ≠ π/2±kπ |